Induction
CSE 16: Applied Discrete Mathematics
Instructor: Owen Arden
Winter 2023
Review of proof techniques
Simple proofs
- Counterexamples
- Existence proofs
- Trivial proofs
- Vacuous proofs
Direct proofs
Indirect proofs
- Proof by Contraposition
- Proof by Contradiction
Proof by cases
Problem: what if there are an infinite number of cases?
How many cases?
Theorem: For every positive integer \(n\), \[\sum_{j=1}^{n} j = \dfrac{n(n+1)}{2}\]
Proof.
- Case 1: \(n=1\).
Need to prove \(\displaystyle\sum_{j=1}^{1} j = \dfrac{1(1+1)}{2}\)
\[\begin{align} 1 &= \dfrac{1(1+1)}{2} \\ 1 &= \dfrac{2}{2} \ \\ 1 &= 1 \end{align}\]
- Case ?: Now what?
Proving infinite cases
How can we prove properties about an infinite number of cases using a finite number of steps?
We couldn’t effectively split up the natural numbers into finite cases since each \(n=1\) gives a slightly different sum.
We need a way to prove the cases more abstractly so they apply to all numbers.
Mathematical induction
Induction is a powerful proof technique that is particularly useful for proving statements about elements in a sequence.
Suppose we want to prove \(P(n)\) for all natural numbers \(n\). There are two components of an inductive proof:
The base case establishes that the theorem is true for the first or “least” value in the sequence. (\(n=1\))
The inductive step establishes that if the the theorem is true for \(n=k\), then it also holds for \(n=k+1\).
- In other words, the inductive step establishes \(P(k) \to P(k+1)\) for an arbitrary \(k\).
- \(P(k)\) is called the inductive hypothesis since we can assume \(P(k)\) holds when proving \(P(k+1)\).
The well-ordered set
- Well ordered
- A set is well ordered if every subset has a least element.
- Well-ordered sets:
- \(\mathbb{N}\)
- \(\mathbb{Z}^{+}\) (positive integers)
- Finite alphabetic strings with lexicographic ordering. (e.g. a,b,…,aa,ab,…)
Using the well-ordered property
Theorem (Division algorithm): If \(a\) is an integer and \(d\) is a positive integer, then there are unique integers \(q\) and \(r\) with \(0 \leq r \lt d\) such that \(a = dq + r\).
Proof. Let \(S\) be the set of nonnegative integers of the form \(a - dq\), where \(q\) is an integer. The set is nonempty since we can make \(dq\) as small or large as necessary.
Since any subset of non-negative integers is well ordered, \(S\) has a least element \(r = a - dq_0\). Since \(r \in S\), it is non-negative. Also, \(r < d\), since otherwise there would be a smaller non-negative element in \(S\): \[a - d(q_0 + 1) = a - dq_0 - d = r - d > 0\]
Therefore, there are unique integers \(q\) and \(r\) with \(0 \leq r \lt d\). \(\square\)
Induction
Mathematical induction is an inference rule that is valid because of the well-ordering property.
Theorem (Mathematical induction): \(P(n)\) is a statement parameterized by a positive integer \(n\). \[(P(1) \wedge \forall k. P(k) \to P(k+1)) \to \forall n. P(n)\] where the domain of \(k\) is the positive integers.
In other words, if you prove \(P(1)\) and \(P(k) \to P(k+1)\), then \(P(n)\) is true for all \(n\).
Proof of induction theorem
Suppose \(P(1)\) and \((P(k) \to P(k+1)\) for all \(k \in \mathbb{Z}^{+}\).
Assume for contradiction there is at least one positive integer \(n\) such that \(P(n)\) is false. Let \(S\) be the set of all positive integers \(x\) where \(\neg P(x)\). Then \(S\) is non-empty since \(n \in S\).
Since \(\mathbb{Z}^{+}\) is well-ordered, \(S\) has a least element we will call \(m\).
Since \(P(1)\) is true by assumption, \(m \neq 1\).
Since \(m\) is positive and greater than \(1\), \(m-1\) is a positive integer.
Since \(m\) is the least element of \(S\), \(m-1 \not\in S\), so \(P(m-1)\) is true.
But since \(P(k) \to P(k+1)\) is true (by assumption), \(P(m-1)\) implies \(P(m)\), a contradiction.
Therefore \(P(n)\) is true for all \(n \in \mathbb{Z}^{+}\).\(\square\)
Using induction
Theorem: For every positive integer \(n\), \[\sum_{j=1}^{n} j = \dfrac{n(n+1)}{2}\]
Proof. We prove the theorem by induction on \(n\).
- Base case \((n=1)\).
We need to prove \(\displaystyle\sum_{j=1}^{1} j = \dfrac{1(1+1)}{2}\) \[\begin{align} 1 &= \dfrac{1(1+1)}{2} \\ 1 &= \dfrac{2}{2} \ \\ 1 &= 1 \end{align}\]
Using induction
Theorem: For every positive integer \(n\), \[\sum_{j=1}^{n} j = \dfrac{n(n+1)}{2}\]
Proof. We prove the theorem by induction on \(n\).
- Inductive step.
Assume \(\displaystyle\sum_{j=1}^{k} j = \dfrac{k(k+1)}{2}\). We need to prove \(\displaystyle\sum_{j=1}^{k+1} j = \dfrac{(k+1)(k+2)}{2}\).
\[\begin{align} \sum_{j=1}^{k+1} j &= \sum_{j=1}^{k} j + (k+1) & \qquad \text{defn. of summ.} \\ &= \dfrac{k(k+1)}{2} + (k+1) & \qquad \text{by inductive hyp.} \\ &= \dfrac{k(k+1)+ 2(k+1)}{2} & \qquad \text{by algebra} \\ &= \dfrac{(k+2)(k+1)}{2} & \qquad \text{by algebra} \end{align}\]
Using induction
Theorem: For every positive integer \(n\), \(n \lt 2^{n}\).
Proof.
Base case \((n=1)\): True since \(1 < 2^{1} = 2\).
Inductive step:
- Assume \(k \lt 2^{k}\) for positive integer \(k\).
- Since \(k \lt 2^{k}\), \(k+1 \lt 2^{k} + 1\).
- Then \(2^{k} + 1 \leq 2^{k} + 2^{k} = 2 \cdot 2^{k} = 2^{k+1}\)
Therefore, \(n \lt 2^{n}\) holds for all positive integers \(n\).\(\square\)
Using induction
Theorem: Suppose \(S\) is a finite set with \(n\) elements, where \(n\) is a non-negative integer. Then \(S\) have \(2^{n}\) subsets.
Proof.
Base case \((n=0)\): True since the empty set has only itself as a subset and \(2^0=1\).
Inductive step: Let \(S\) have \(k\) elements (\(|S|=k\)).
- Assume \(S\) has \(2^k\) subsets for an arbitrary nonnegative integer \(k\).
- Let \(S' = S \cup \{a\}\). We want to prove that \(S'\) has \(2^{k+1}\) subsets.
- For each subset \(X\) of \(S\), there are exactly two subsets of \(T\): \(X\) and \(X \cup \{a\}\).
- Since \(S\) has \(2^k\) subsets (by the IH), \(S'\) has \(2*2^k = 2^{k+1}\). \(\square\)
Fibonacci sequence
What if the induction hypothesis isn’t enough?
Consider the Fibonacci sequence, where \(f_0=0, f_1=1\) and for \(n \geq 2\): \[f_n = f_{n-1} + f_{n-2}\] Prove that \(f_n \leq 2^{n}\) for all \(n\).
- Inductive case(s)?
- Assume \(f_k < 2^k\), prove \(f_{k+1} \leq 2^{k+1}\).
- \(f_{k+1} = f_{k} + f_{k-1}\)
- Is \(f_{k-1}\) less than or equal to \(2^{k-1}\)???
- Need a stronger induction hypothesis!
Strong induction
Theorem (Strong induction): \(P(n)\) is a statement parameterized by a positive integer \(n\). Let \(a \leq b\) be integers. Then \(P(n)\) is true for all \(n \geq a\), if:
- \(P(a), P(a+1), ..., P(b)\) are true.
- For all \(k \geq b\), \[(P(a) \wedge P(a+1) \wedge ... \wedge P(k)) \to P(k+1)\]
Fibonacci sequence
Consider the Fibonacci sequence, where \(f_0=0, f_1=1\) and for \(n \geq 2\): \[f_n = f_{n-1} + f_{n-2}\] Prove that \(f_n \leq 2^{n}\) for all \(n\).
- Base cases: \(a=0,b=1\)
- \(0 \leq 2^0 = 1\)
- \(1 \leq 2^1 = 2\)
- Inductive step:
- Assume for all \(k \geq a\), \(f_k \leq 2_{k}\), so then \(f_{k-1} \leq 2_{k-1}\).
- Then \[f_{k+1} = f_{k} + f_{k-1} \leq 2_{k} + 2_{k-1} \leq 2_{k} + 2_{k} = 2^{k+1}\]
Recursively defined functions
Fibonacci numbers are an example of recursively or inductively defined functions. These definitions share some structure with inductive proofs:
- Recursive function
- A recursive or inductive function definition has two steps:
-
- The basis step specifies the value of the function at specific domain elements (e.g., 0).
-
- The recursive step gives a rule for finding the value of the function at a domain element using the function value(s) at smaller elements.
Recursively defined functions
Example: Suppose \(f(0)=3\) and \(f(n+1) = 2*f(n)+3\). Find \(f(4)\).
Solution: \[\begin{align} f(4) &= 2*f(3) + 3 = 2*45 + 3 = 93 \\ f(3) &= 2*f(2) + 3 = 2*21 + 3 = 45 \\ f(2) &= 2*f(1) + 3 = 2*9+3 = 21 \\ f(1) &= 2*f(0) + 3 = 9 \end{align}\]
Recursively defined sets
- Recursive definitions of sets
-
- The basis step specifies an initial collection of elements.
-
- The recursive step gives rules for forming new elements in the set from elements already known to be in the set.
Recursively defined sets
Example: Define \(S\) to be a subset of the integers as:
- Basis step: \(3 \in S\).
- Recursive/Inductive step: If \(x \in S\) and \(y \in S\), then \(x+y \in S\).
What are some elements of \(S\)?
\(3, 6, 9\) etc.
Example: The natural numbers \(\mathbb{N}\).
- Basis step: \(0 \in \mathbb{N}\).
- Inductive step: If \(n \in \mathbb{N}\), then \(n+1 \in \mathbb{N}\).
Strings
We can also define other structures recursively.
- Strings
- Let \(\Sigma\) be a set of symbols (an alphabet). The set \(\Sigma^{*}\) of strings over \(\Sigma\) is defined:
-
- \(\lambda \in \Sigma^{*}\). (\(\lambda\) is the empty string)
-
- If \(w \in \Sigma^{*}\) and \(x \in \Sigma\), then \(wx \in \Sigma^{*}\).
Example: If \(\Sigma = \{0,1\}\), then \(\Sigma^{*}\) is the set of all binary strings: \(\lambda, 0, 1, 00,01,10,11\), etc.
Example: If \(\Sigma = \{a,b\}\), show that \(aab\) is in \(\Sigma^{*}\).
- Since \(\lambda \in \Sigma^{*}\) and \(a \in \Sigma\), then \(a \in \Sigma^{*}\).
- Since \(a \in \Sigma^{*}\) and \(a \in \Sigma\), then \(aa \in \Sigma^{*}\).
- Since \(aa \in \Sigma^{*}\) and \(b \in \Sigma\), then \(aab \in \Sigma^{*}\).
Functions on inductively defined structures
To specify functions on inductive structures (like strings), we also use inductive definitions:
Define \(B=\{0,1\}\) and let \(B^{*}\) be the set of all strings over \(B\). The length of a string \(w \in B^{*}\), written \(|w|\), is defined as:
- \(|\lambda| = 0\)
- If \(x \in B^{*}\), then \[\begin{align} |x0|&=|x|+1 \\ |x1|&=|x|+1 \end{align}\]
Well-formed propositional formulae
Let \(\mathcal{F}\) be the set of well-formed formulae in propositional logic, involving \(\text{T}\), \(\text{F}\), propositional variables, and operators \(\neg,\wedge,\vee,\to,\leftrightarrow\).
- \(\text{T},\mathcal{F}\), and \(s\), are in \(\mathcal{F}\), where \(s\) is a propositional variable.
- If \(P\) and \(Q\) are in \(\mathcal{F}\), then \((\neg P)\), \((P \wedge Q)\), \((P \vee Q)\), \((P \to Q)\), \((P \leftrightarrow Q)\), are also in \(\mathcal{F}\).
- \(((p \vee q) \to (q \wedge \text{F}))\)
- \(((p \vee) \to\)
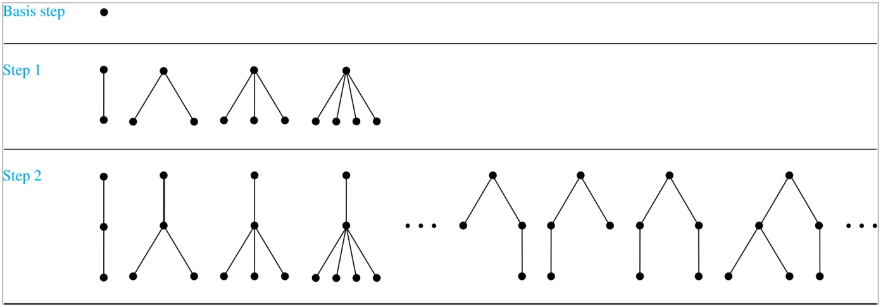
Rooted trees
An inductive definition of rooted trees:
- A single vertex \(r\) is a rooted tree.
- If \(T_1, T_2, ..., T_n\) are disjoint rooted trees with roots \(r_1, r_2, ..., r_n\), respectively, then the graph formed by starting with a root \(r\) such that \(\forall i. r \not\in T_i\), and adding an edge from \(r\) to each of \(r_1, r_2, ..., r_n\), is also a rooted tree.
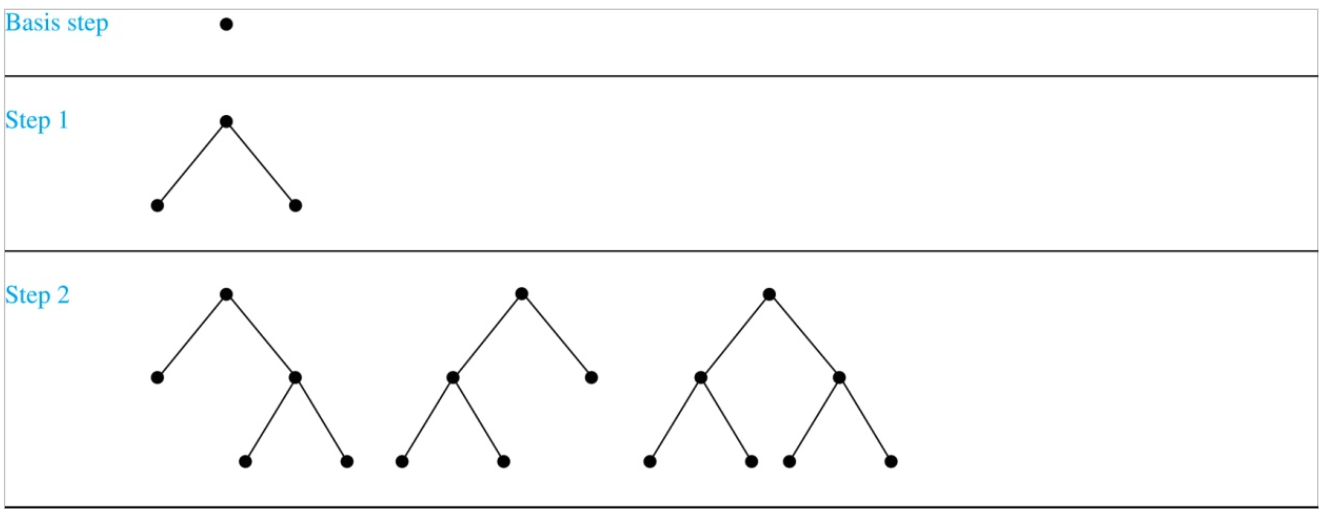
Full binary trees
An inductive definition of full binary trees:
- A single vertex \(r\) is a full binary tree.
- If \(T_1\) and \(T_2\) are disjoint full binary trees with roots \(r_1, r_2\), respectively, then the graph formed by starting with a root \(r\) such that \(\forall i. r \not\in T_i\), and adding an edge from \(r\) to each of \(r_1, r_2, ..., r_n\), is also a full binary tree.